The application has two PID (Proportional-Integral-Derivative) filters designed to set their parameters in ranges of different orders of magnitude. Also, the PIDs are combined with auxiliar adders and a multiplexer that makes the system suitable for scanning and loop-back schemes of control.
The PID module design
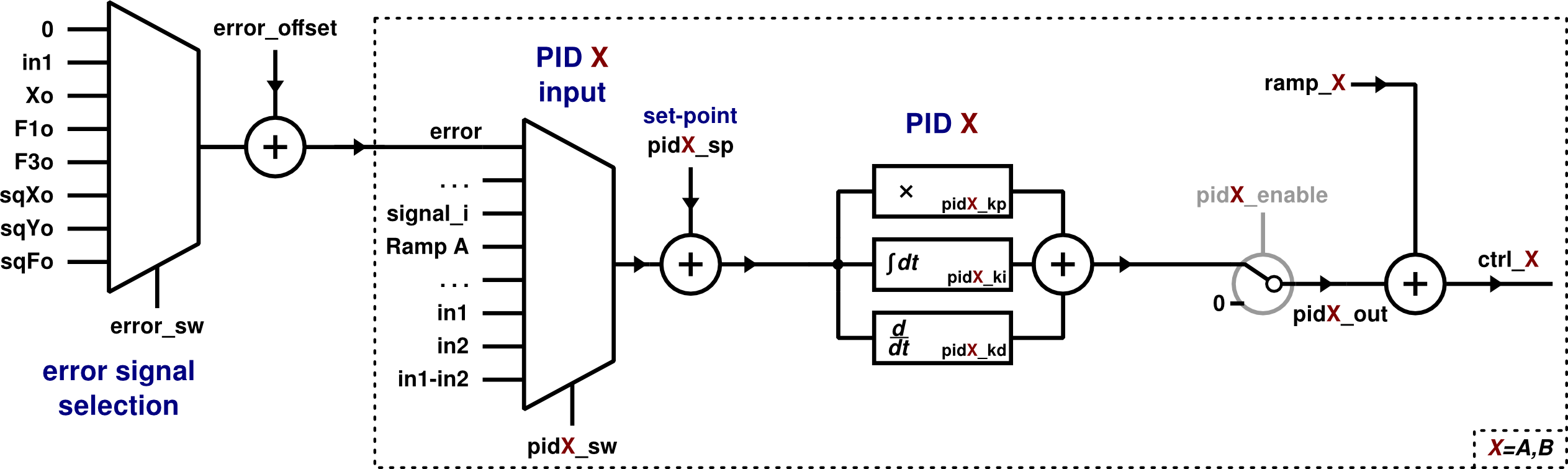
Each PID filter has a multiplexer for input signal selection, controlled
by pidX_sw parameter.
pidA_sw and pidB_sw lets you choose from these input signals:
error,
Xo,
Yo,
F1o,
F2o,
F3o,
sqXo,
sqYo,
sqFo,
signal_i,
ramp_A,
sin_ref,
cos_ref,
cos_1f,
cos_2f,
cos_3f,
sq_ref,
sq_quad,
sq_phas,
aux_A,
aux_B,
test14,
in1,
in2,
in1-in2.
All the signals are 14 bit signed int (range:[-8192:8191]).
The input signal is processed by the PID filter itself, and the output is:
\[out = k_p \cdot (sp-in) + k_i \cdot \int_0^t{ (sp-in) dt } + kd \cdot \frac{d}{dt}(sp-in)\]where \(in\) is te input signal pidX_in, \(sp\) is the set-point value pidX_sp,
\(k_p = \frac{\color{var}\texttt{pidX_kp}}{ scale }\),
\(k_i = \frac{\color{var}\texttt{pidX_ki}}{ \tau_i }\) and
\(k_d = \frac{\color{var}\texttt{pidX_kd}}{ \tau_d }\).
There are another 3 boolean parameters for state control of each PID. They are:
pidX_irst (reset integral), pidX_freeze (freeze out) and pidX_ifreeze (freeze integral).
The first one sets the integral memory to zero while is on, but proportional an derivative terms are kept
actives.
The second one freezes the output value of the whole PID and keeps this value while the parameter is True.
The third parameter freeze only the integral term, keeping proportional and derivative active. It’s
useful to stop the integral behavior to test a system without making an instantaneous jump to zero in
the PID output.
Error signal
The default input signal for both PIDs is the error signal, that can be selected
from several inputs using the error_sw parameter, and can be byased by an error_offset amount
for set-point purposes.
This feature ease the signal conditioning tuning for schemes of two PIDs working with the same input.
The error signal is used in other panels features.
Proportional
The proportional part of the PID is set by two parameters: pidX_kp and pidX_PSR.
The first one is the proportionality factor. The second one a scale to change order of magnitude of the
amplification.
pidX_PSR lets you choose the value of \(scale\) from this options: 1, 8, 64, 1024, 4096. The default value is
- This option is hidden by default and appears turning on the “More options” button.
With the default scale, if you set pidA_kp=512 the proportional part of PID A will output a signal with the half
of the amplitude of the input.
Integral
The integral part of the PID is set by two parameters: pidX_ki and pidX_ISR.
The first one is the proportionality factor. The second one a scale to change order of magnitude of the
characteristic time of the integrator \(\tau_i\).
pidX_ISR lets you choose the value of \(\tau_i\) from this options:
8 ns,
64 ns,
512 ns,
8 us,
6 us,
524 us,
8 ms,
67 ms,
537 ms,
9 s. The default value is
537 ms. This option is hidden by default and appears turning on the “More options” button.
With the default scale, if you set pidA_ki=3 the integral part of PID will have a characteristic time of:
This means that if the input is a signal of 1 V constant and the integrator starts at 0 V, the output will start raising at \(\frac{1}{179}\) V/ms and will reach 1 V at 179 ms later.
Derivative
Web Frontend
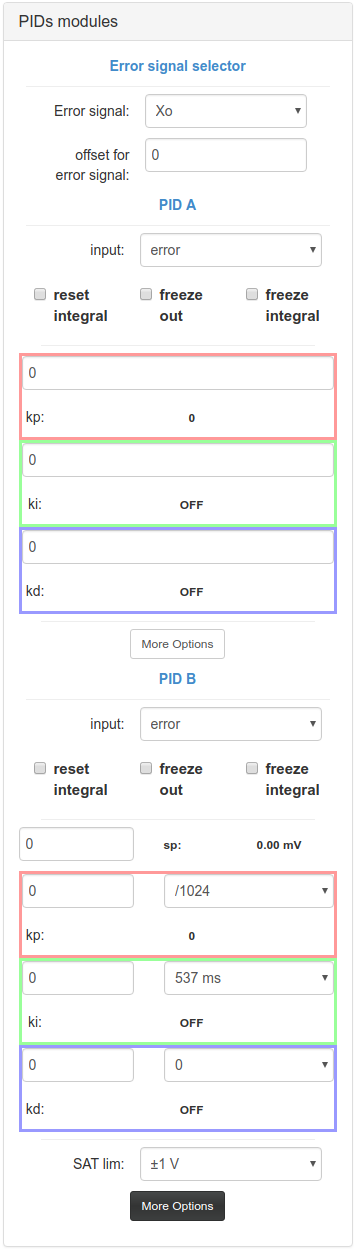
The figure shows the controls used to set the FPGA parameters. The basic interfase for PID A and the “More Options” interfase for PID B.